
➕ Matemática MozEstuda
32.7K subscribers
About ➕ Matemática MozEstuda
Estude Matemática com MozEstuda 🇲🇿 www.mozestuda.com
Similar Channels
Swipe to see more
Posts

APRENDER NÃO OCUPA ESPAÇO 📝🧠 *LOGARITMO.* _Deixe aquele coração ❤️💓👍✊_


*EQUAÇÃO EXPONENCIAL.* Uma equação exponencial é uma equação em que a incógnita aparece no expoente de uma base elevada a uma potência. Ela pode ser escrita na forma geral a^x = b, onde "a" é a base da potência, "x" é o expoente desconhecido e "b" é o resultado da potência. Para resolver uma equação exponencial, geralmente utilizamos propriedades das potências para simplificar a expressão. Uma das propriedades mais comuns é a seguinte: se a^x = a^y, então x = y. Isso significa que se as bases são iguais, os expoentes também devem ser iguais. Vamos utilizar um exemplo para ilustrar como resolver uma equação exponencial: Exemplo: Resolver a equação 2^x = 16 Neste caso, podemos observar que 16 pode ser reescrito como 2^4, já que 2 elevado a 4 é igual a 16. Portanto, a equação 2^x = 16 pode ser reescrita como 2^x = 2^4. Como as bases são iguais, podemos igualar os expoentes: x = 4 Portanto, a solução para a equação 2^x = 16 é x = 4. É importante lembrar que nem sempre as equações exponenciais podem ser resolvidas de forma simples e direta. Em alguns casos, é necessário utilizar logaritmos para resolver a equação. Além disso, é fundamental estar atento às propriedades das potências e praticar bastante para se familiarizar com esse tipo de equação.
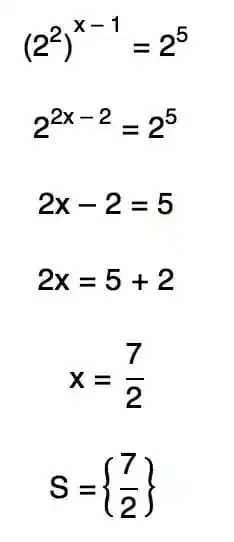

*EQUAÇÃO LOGARÍTMICA* Uma equação logarítmica é uma equação que contém uma ou mais funções logarítmicas. Para resolver uma equação logarítmica, você precisa isolar o logaritmo em um dos lados da igualdade e então usar propriedades dos logaritmos para simplificar a equação e encontrar a solução. Vamos considerar um exemplo simples de uma equação logarítmica: log₃(x) = 2 Para resolver esta equação, primeiro vamos aplicar a definição de logaritmo: 3^2 = x 9 = x Portanto, a solução da equação logarítmica log₃(x) = 2 é x = 9. Em equações logarítmicas mais complexas, você pode precisar usar propriedades dos logaritmos, como a propriedade da potência e a propriedade da igualdade de logaritmo, para simplificar a equação antes de resolver. Lembre-se de sempre verificar se a solução encontrada é válida substituindo-a de volta na equação original e certificando-se de que ela satisfaz a igualdade.
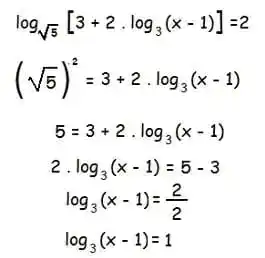

https://youtube.com/@mozestuda?sub_confirmation=1

Aprender não ocupa espaço 🧠🧠📝🧠 *Notação científica.*


Matemática Sumário: *RACIONALIZAÇÃO DOS DENOMINADORES*. A racionalização dos denominadores é um processo utilizado na simplificação de expressões algébricas em que os denominadores das frações possuem raízes quadradas, cubos, ou qualquer outro tipo de radical. O objetivo é eliminar esses radicais do denominador, tornando a expressão mais simplificada e de mais fácil manipulação. Para racionalizar um denominador, podemos utilizar algumas técnicas diferentes, dependendo do tipo de radical presente. Vamos ver a seguir as principais técnicas para racionalização dos denominadores: 1. Radicais simples: Quando temos um radical simples, como por exemplo √2, no denominador de uma fração, podemos multiplicar tanto o numerador quanto o denominador por esse mesmo radical. Assim, conseguimos eliminar o radical do denominador. Por exemplo: 1/√2 = (1/√2) * ( √2/√2) = √2/2 2. Radicais duplos: Se o denominador contém um radical duplo, como por exemplo √3, podemos multiplicar tanto o numerador quanto o denominador por esse mesmo radical, mas precisamos multiplicar também pelo conjugado do radical. O conjugado de um radical é obtido trocando o sinal da parte imaginária (se houver) do radical. Por exemplo: 1/(√3 + √2) = (1/(√3 + √2)) * (√3 - √2)/(√3 - √2) = (√3 - √2)/(3-2) = √3 - √2 3. Radicais cubos: Para racionalizar denominadores com raízes cúbicas, como por exemplo ∛5, podemos multiplicar tanto o numerador quanto o denominador por um fator adequado que elimine o radical do denominador. Em casos de raízes cúbicas, é necessário multiplicar pelo quadrado do radical correspondente. Por exemplo: 1/∛5 = (1/∛5) * (∛5²/∛5²) = ∛5²/5 = ∛25/5 = 5/5 = 1 Essas são as técnicas básicas para racionalização dos denominadores em expressões algébricas. É importante lembrar de sempre simplificar ao máximo as expressões, eliminando fatores comuns e reduzindo as frações o máximo possível.


https://youtu.be/1zSHpOSeQoo?si=3qm_noqu4sza6tfr

https://youtube.com/@mozestuda?si=YPT6PDgWX7ZxvjGV *Siga-nos também no YouTube*👍☝️☝️☝️ Entre e subscreva-se

*_Aprender não ocupa espaço 📝🧠🧠🧠_*


https://youtu.be/UEkdNYgtxQ4?si=gt-XbEr8W7ks0A0P














